Pelayananpublik.id- Bagi Anda yang sedang belajar metematika,pasti sudah tidak asing lagi dengan istilah vektor. Perhitungan vektor berkaitan dengan nilai dan arah sehingga simbolnya adalah berbentuk panah seperti menunjuk arah.
Dalam matematika vektor digambarkan dalam bentuk garis lurus yang mempunyai panjang dan arah.
Vektor sendiri ditemukan oleh mobius pada 1827. Saat itu Mobius mempublikasikan Der Barycentrische Calcul, sebuah buku geometri yang mengkaji transformasi garis dan irisan kerucut. Fitur baru dalam hasil karya ini adalah pengenalan koordinat barycentric.

Diberikan sembarang segitiga ABC maka jika garis berat a, b, dan c berturut-turut dilukis pada A, B, dan C maka dapat ditentukan sebuah titik P, yaitu titik berat segitiga.
Mobius memperlihatkan bahwa setiap titik P pada bidang datar ditentukan oleh koordinat homogen [a,b,c]. Garis – garis berat yang diperlukan diletakkan pada A,B, dan C untuk menentukan titik berat P. Yang terpenting disini adalah pandangan Mobius tentang besaran berarah, sebuah pemunculan awal mengenai konsep vektor.
Pada tahun 1837 Mobius mempublikasikan buku tentang statika di mana ia secara gamblang menyatakan idenya tentang penyelesaian masalah besaran vektor bersama dengan dua sumbu koordinat.
Di antara dua hasil karya Monius ini, sebuah karya tentang geometri oleh Bellavitis dipublikasikan tahun 1832 yang juga membahas besaran yang merupakan vektor. Odjek dasarnya adalah segmen garis AB dan ia memandang AB dan BA sebagai dua objek yang berbeda. Ia mendefinisikan dua segmen garis sebagai ‘equipollent’ jika keduanya sama panjang dan paralel. Dalam notasi modern, dua segmen garis adlah equipollent jika keduanya mewakili dua vektor yang sama.
Kini vektor menjadi salahsatu materi yang dipelajari dalam matematika di sekolah. Vektor ini merupakan subjek familiar di kalangan siswa sekolah.Penggambaran vektor berbentuk panah yang menunjukan arah vektor dan panjang garisnya disebut sebagai besar vektor.
Misalkan sebuah vektor Z yang berawal dari titik A(x_1,y_1) menuju titik B(x_2,y_2) dapat digambarkan koordinat cartesius dibawah. Panjang garis sejajar sumbu x adalah v_1 = x_2 – x_1 dan panjang garis sejajar sumbu y adalah v_2 = y_2 – y_1 merupakan komponen-komponen vektor Z.
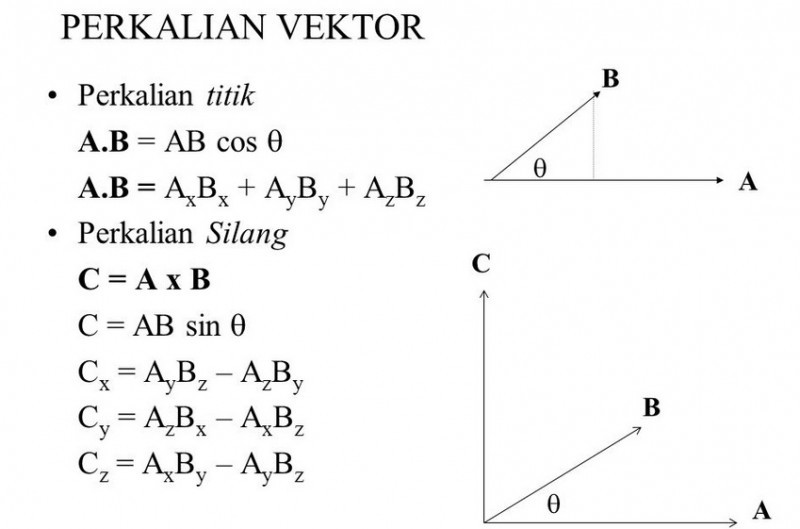
Vektor memiliki sifat yakni dapat dipindahkan, dijumlahkan, dikurangkan, diuraikan dan dikalikan.
Menulis Notasi Vektor
Berikut ini adalah cara menuliskan notasi vektor. Bentuk penulisan simbol vektor dapat dilakukan dengan dua cara, yaitu sebagai berikut:
1. Disimbolkan dengan 2 huruf besar. Kemudian diberi tanda anak panah diatasnya.
2. Disimbolkan dengan 2 huruf besar yang penulisannya ditebalkan.
Jenis Vektor
1. Vektor Nol
Vektor Nol adalah suatu vektor yang panjangnya nol dan dinotasikan \bar{0}. Vektor nol tidak memiliki arah vektor yang jelas.
2. Vektor Posisi
Vektor Posisi adalah suatu vektor yang posisi titik awalnya berada di titik 0 (0,0) dan titik ujungnya berada di titik A (a_1,a_2).
3. Vektor satuan
Vektor satuan merupakan vektor yang panjangnya satu satuan. Vektor satuan dari \vec{v} = \left(\begin{array}{r} v_1\\ v_2\end{array}\right) adalah:
\bar{U_v} = \frac{\bar{v}}{\mid\bar{v}\mid} = \frac{1}{\mid\bar{v}\mid}\left(\begin{array}{r} v_1\\ v_2\end{array}\right)
4. Vektor
Vektor basis adalah suatu vektor yang satuannya saling tegak lurus. Misalkan dalam vektor ruang dua dimensi (R^2) memiliki dua vektor basis yaitu \bar{l} = (1,0)dan \bar{j} = (0,1).
Dalam ilmu fisika juga ada pembahasan mengenai vektor. Vektor terbagi dua, vektor sejajar adalah dua vektor atau lebih yang memiliki arah serta juga besar yang sama. Vektor berlawanan adalah dua atau lebih vektor yang memiliki besar yang sama namun arahnya berlawanan.
Berdasarkan Operasinya
a. Vektor Penjumlahan
Penjumlahan vektor adalah menentukan sebuah vektor yang kompononenya adalah jumlah dari kedua komponen vektor pembentuknya, menentukan resultan dari 2 vektor. Ada 2 jenis vektor dalam penjumlahan vektor, yaitu Vektor Segaris dan Vektor Tidak Segaris.
b. Vektor Pengurangan
Pengurangan vektor adalah salah satu vektor yang mempunyai atau memiliki arah yang berlawanan. Contohnya : Misalkan Vektor A bergerak ke arah kanan dan Vektor B bergerak ke arah kiri, maka resultannya adalah R = A + (-B) = A – B.
Pada penjumlahan vektor terdapat sifat komutatif dan asosiatif, sedangkan untuk pengurangan dua buah vektor tidak berlaku dua sifat tersebut.
Demikiaan ulasan mengenai pengertian vektor.Semoga bermanfaat. (*)